RでChangeFinder
変化点検出のアルゴリズムとして、ChangeFinderという有名なアルゴリズムがあります。Rによる実装例が見つからなかったので実装しました。今回は1次元のデータに対する変化点検出を考えます。アルゴリズムの詳細は記述しませんので、後述の参考群を参照してください。
実装
まず、準備として予め2つの関数を定義しておきます。
1つ目は、アルゴリズム内で用いる平滑化用の関数です。
2つ目は、擬似逆行列を計算する関数です。計算上、逆行列が存在しない場合もありますので、擬似逆行列を計算する必要があります。今回はムーア・ペンローズ逆行列を実装しています。
## 平滑化用関数 MW <- function(dat, width, na.rm = TRUE) { N <- length(dat) x <- numeric(N) for(i in 1L:(width-1L)) { x[i] <- mean(dat[1L:i], na.rm = na.rm) } for(i in width:N) { x[i] <- mean(dat[(i-width+1L):i], na.rm = na.rm) } return(x) } ## 擬似逆行列計算用関数(MASSパッケージより) ginv <- function (X, tol = sqrt(.Machine$double.eps)) { if (length(dim(X)) > 2L || !(is.numeric(X) || is.complex(X))) stop("'X' must be a numeric or complex matrix") if (!is.matrix(X)) X <- as.matrix(X) Xsvd <- svd(X) if (is.complex(X)) Xsvd$u <- Conj(Xsvd$u) Positive <- Xsvd$d > max(tol * Xsvd$d[1L], 0) if (all(Positive)) Xsvd$v %*% (1/Xsvd$d * t(Xsvd$u)) else if (!any(Positive)) array(0, dim(X)[2L:1L]) else Xsvd$v[, Positive, drop = FALSE] %*% ((1/Xsvd$d[Positive]) * t(Xsvd$u[, Positive, drop = FALSE])) }
ChangeFinderの要の部分になります。ARで定めた時系列モデルからの逸脱度を計算します。さらにこのアルゴリズムはオンラインアルゴリズムであるため、忘却係数を用いたパラメータの更新も行います。スコア計算には対数損失を用いています。
SDAR1 <- function(x, ar_order, forgetting, mu = 0, co = numeric(ar_order+1), w = numeric(ar_order), S = 0) { N <- length(x) score <- numeric(N) for(t in (ar_order+1L):N) { mu <- (1-forgetting)*mu + forgetting*x[t] co <- (1-forgetting)*co + forgetting*(x[t]-mu)*(x[t-(0:ar_order)]-mu) w <- c(ginv(matrix(co[abs(rep(1:ar_order, ar_order)-rep(1:ar_order, each=ar_order))+1], ar_order, ar_order)) %*% co[-1]) x_hat <- c(w %*% (x[t-(1:ar_order)]-mu)) + mu S <- (1-forgetting)*S + forgetting*(x[t]-x_hat)^2 score[t] <- (log(2*pi*S) + (x[t] - x_hat)^2 / S) / 2 } list(Score = score, x = x) }
いよいよChangeFinderアルゴリズムの完成になります。SDARと平滑化を繰り返すのみですので、ここは簡潔に済みます。
またここで、パラメータの第1Step・第2Stepの初期値をどうするかという問題があるのですが今回はすべて0としています。
CF <- function(x, ar_order, forgetting, width1, width2 = width1, na.rm = TRUE) { Step1 <- SDAR1(x, ar_order, forgetting)$Score Step2 <- MW(Step1, width1, na.rm) Step3 <- MW(SDAR1(Step2, ar_order, forgetting)$Score, width2, na.rm) return(Step3) }
適用例
シミュレーションにはF# でオンライン変化点検知 - 捨てられたブログの例を利用しています。
x <- c(rnorm(300, 0.7, 0.05), rnorm(300, 1.5, 0.05), rnorm(300, 0.6, 0.05), rnorm(300, 1.3, 0.05)) CF_test <- CF(x, 1, 0.01, 7, 7) plot(x, col = rep(c(1:2, 1:2), each = 300), ylim = range(x, CF_test)) lines(CF_test, col = 4)
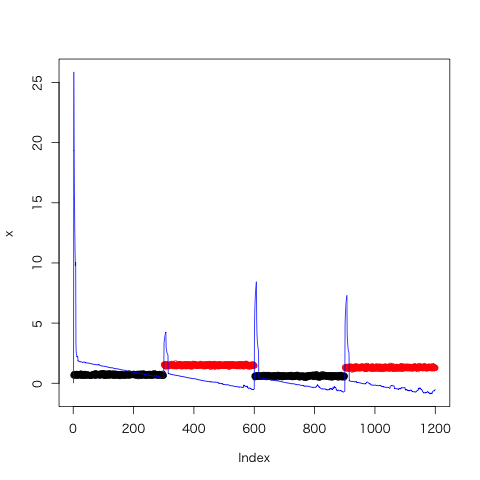
青線を変化点スコア、黒点及び赤点を時系列データとしています。上図を見ると変化点スコアが初めの方で大きく伸びていますが、これはパラメータの初期値が関係しています。対策としては、時系列データの幾分かを学習データとして与えることでスコアをより適切にすることができます。
参考
- 変化点検出 ChangeFinder
- F# でオンライン変化点検知 - 捨てられたブログ
- changefinder - Argmax.jp
- 一般逆行列・ムーア・ペンローズ逆行列 - 大人になってからの再学習

- 作者: 山西健司
- 出版社/メーカー: 共立出版
- 発売日: 2009/05/23
- メディア: 単行本
- 購入: 3人 クリック: 29回
- この商品を含むブログ (5件) を見る