Rで単純パーセプトロンを組んでみた

SVMを実装するにあたって「まずパーセプトロンを組んでみては？」と先輩からアドバイスを頂いたので、実装してみた。パーセプトロンに関するまとめ付き。

機械学習としてのパーセプトロン

　機械学習は、大きく3種類に分けて考えることができる。*1

識別関数: 入力データを見て、特定のクラスに属するように識別する
識別モデル: 入力データからクラス事後確率をモデル化して識別する
生成モデル: 入力データが生成される確率分布をモデル化して識別する

　今回学んだパーセプトロンは「識別関数」に該当し、その中でも最も基本的な線形識別器である。しかし最も基本的であるからといって、識別能力が低いというわけではない。
　また今後学ぶSVMは(大雑把に言うと)、このパーセプトロンという識別関数に「マージン最大化」と「カーネル関数」を取り入れたものであるらしい。

　パーセプトロンは2クラスのクラス分類器のこと。どんな識別関数かというと、下式で表すような線形識別関数である。
${ \displaystyle \begin{align} y=w^Tx \end{align} }$
${w}$ は重みベクトル、 $x$ は入力ベクトルであり、これらの内積が0より小さいかそれ以上かでクラス分類をしている。この説明だともしかしたら下式の方が理解しやすいかもしれないので、こちらも示しておく。
${ \displaystyle \hat{y} = \left\{ \begin{array}{ll} +1 & (w^Tx\ge 0) \\ -1 & (w^Tx<0) \end{array}\right.}$
パーセプトロンではこの重みベクトル $w$ を変化させることで、適切なクラス分類をしたい。
　入力データの教師ラベル $t_i\ (1\le i \le N)$ が、クラス1( $C_1$ )の時+1、クラス2( $C_2$ )のとき-1であるとすると、正しく分類されていることは下の条件を満たすことに等しい。
$\displaystyle w^T x_i>0\ \ \ (x_i\in C_1)\\ w^T x_i<0\ \ \ (x_i\in C_2)$
これらをまとめると、下式で表すことができる。
$\displaystyle w^T x_i\times t_i>0$
　さて、この式によってどのデータを誤判別しているかどうかがわかるようになったので、次は誤判別しているデータがどのくらい分離超平面と距離があるのかを考えることで、分離超平面の「ズレ」具合を数値として求める。パーセプトロンでは、この「ズレ」具合をヒンジ損失関数 ${l_k(w, x, y)}$ を用いて以下のように表す。（ $k$ はステップ数）
$\displaystyle l_k(w, x_i, t_i)=max(0, −w^Tx_i\times t_i)$
さらにこれを用いて、 $w$ に関する誤差関数（パーセプトロン規準*2）を求める。
$\displaystyle E_p(w)=\sum_{i=1}^{N}{l_k(w, x_i, t_i)}$
この誤差関数は誤判別データからの「ズレ」の和であるから、これを最小化するような $w$ を求めることができれば、適切にデータを分類できるかもしれない。誤差関数の最小化には、確率的最急降下法（詳しくはここ）より下式を用いて $w$ を逐次的に更新する。
$\displaystyle \begin{eqnarray*} w_{k+1}&=&w_k−\mu\nabla E_p(w)\\ &=&w_k-\mu\frac{\partial l_k}{\partial w}\\ &=&w_k+\mu x_it_i \end{eqnarray*}$
なお、 $\mu$ は学習係数を表す。
　オンライン学習云々については機会があればということで、ここでは省略。

Rによる実装

関数として作成。上では説明していないが、バイアス項も重みベクトルとして含めた。

# mu = 学習係数
perceptron  <- function(x, label, eps=1e-10, mu=0.5, int=0) {
  if(ncol(x)==1 || is.vector(x)) {
    x <- cbind(x, 0, 1)
  }
  else if(ncol(x)==2) {
    x <- cbind(x, 1)
  }
  w <- rep(0, 2)
  k <- 0L
  upperlimit <- TRUE
  x1 <- x[sign(label)==1, 1:2]
  x2 <- x[sign(label)==-1, 1:2]
  plot(x1, xlim=range(x[, 1]), ylim=range(x[, 2]), xlab="x", ylab="y", col=2)
  points(x2, col=3)
  abline(a=w[2], b=w[1], col=gray(0.8))
  while(upperlimit) {
    for(i in 1:nrow(x)) {
      # 学習部 (+ α) <-- ここから
      if((label[i]*((w %*% x[i, c(1, 3)])[1] - x[i, 2])) <= 0) {
        w <- w + mu * label[i] * x[i, c(1, 3)]
        k <- k + 1L
        Sys.sleep(int)
        abline(a=w[2], b=w[1], col=gray(0.8))
      }
      # ここまで -->
    }
    # 終了判定 <-- ここから
    # パーセプトロン規準 <= eps なら終了
    lim <- w[1] * x[, 1] + w[2] * x[, 3] - x[, 2]
    lim <- sum(max(0, -label * lim) / norm(c(w, -1), "2"))
    if(lim <= eps) {
      upperlimit <- FALSE
    }
    # ここまで -->
  }
  abline(a=w[2], b=w[1])
  return(list("intercept"=as.numeric(w[2]), 
              "coefficient"=as.numeric(w[1]), 
              "iteration"=k, 
              "residuals"=lim))
}

実行結果

　完成したperceptron関数を1次元と2次元に対して実行してみた。

1次元

　まずは0~10にばらつく10個の一様乱数に対しての判別から。ラベルは平均より大きいか小さいかで付けている。

x <- runif(10, 0, 10)
perceptron(x=x, label=sign(mean(x)-x))

実行結果と図は以下のとおり。

$intercept
[1] 4.500000

$coefficient
[1] -1.157935

$iteration
[1] 19

$residuals
[1] 0

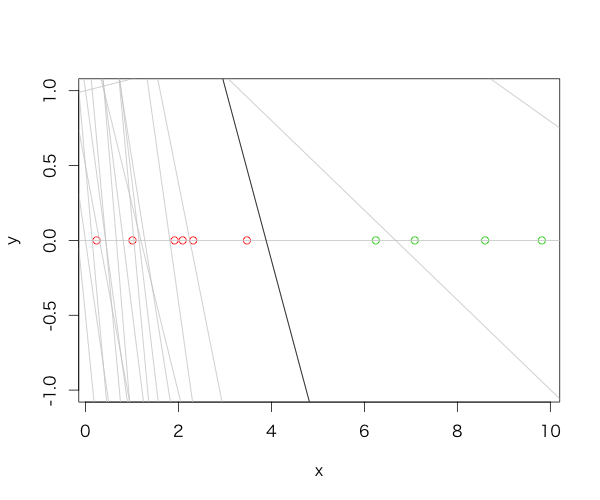
灰色の線は学習途中の分離超平面を表し、黒線が学習完了後の分離超平面を表す。

2次元

　0~1にばらつく100個の一様乱数と、1~2にばらつく100個の一様乱数を分類させた。

N <- 100
x <- rbind(matrix(runif(2*N, 0, 1), nc=2), matrix(runif(2*N, 1, 2), nc=2))
perceptron(x=x, label=rep(c(1, -1), each=N))

実行結果と図は以下。

$intercept
[1] 1.5000000

$coefficient
[1] -0.4656081

$iteration
[1] 13

$residuals
[1] 0

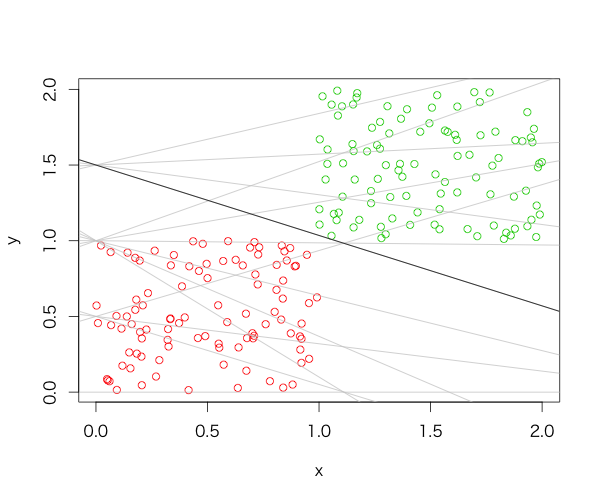
最適とは言えなそうではあるが、入力データに対してはしっかり分類できている様子がわかる。

参考

パターン認識と機械学習上

作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
出版社/メーカー: 丸善出版
発売日: 2012/04/05
メディア: 単行本（ソフトカバー）
購入: 6人クリック: 33回
この商品を含むブログ (16件) を見る

*1:あんちべさんの記事よりほぼ引用

*2:Widrow-Hoffの学習規則という規準もある

J's blog

趣味で統計•データ解析をしています

Rで単純パーセプトロンを組んでみた

機械学習としてのパーセプトロン

パーセプトロンとは

Rによる実装

実行結果

1次元

2次元